Égalités entre RE

Deux relations r_x=(x₁, x₂, x₃) et r_y=(y₁, y₂, y₃) sont égales ssi les trois parties sont respectivement égales. Si x₁, x₂, x₃ et y₁, y₂, y₃ sont des entités positionnées, l'égalité est une relation très forte, puisque elle exige non seulement l'identité de forme entre, par exemple, x₁ et y₁, mais aussi un positionnement identique (si x₂ et y₂ sont des primitives, leur égalité est bien sûr indépendante des positions).

Par exemple, si x₁ est la lexie 'couteau' dans un texte t₁ et y₁ la lexie 'couteau' dans un autre texte t₂, alors r_x et r_y ne peuvent pas être égales.

Nous établissons des identités moins contraignantes que l'égalité pure, fondées sur l'identité par rapport à la référence au corpus des entités positionnées : nous rappelons que ${\text{\sc id}_{ref}}$ (cf. 4.2.4) est appliquée à deux entités positionnées et vérifiée si les deux entités positionnées font référence à la même entité du corpus (e.g. dans le cas des lexies, 'couteau' et 'couteau' dans deux textes différents sont reliées par ${\text{\sc id}_{ref}}$).

Pour la première et la troisième projection d'une RE nous avons :

$$\text{\sc id}_{ref,\pi_1}(r_x, r_y)\Longleftrightarrow{\text{\sc id}_{ref}}(\pi_1(r_x), \pi_1(r_y))$$

$$\text{\sc id}_{ref,\pi_3}(r_x, r_y)\Longleftrightarrow{\text{\sc id}_{ref}}(\pi_3(r_x), \pi_3(r_y))$$

Pour la deuxième projection, il existe deux possibilités selon le type de x₂ : si x₂ elle est une entité positionnée nous avons la même définition que pour les autres projections ; mais s'il s'agit d'une primitive (constante), l'identité est définie simplement à partir de l'égalité des constantes :

$$\begin{array}{ll} \text{Si } & \pi_2(r_x),\pi_2(r_y)\in \math... ...}(r_x, r_y)\Longleftrightarrow\pi_2(r_x)=\pi_2(r_y) \end{array}$$

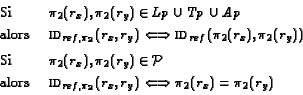
Si les deux deuxièmes projections ($\pi_2$) ne sont pas de même type (i.e. l'une est une entité positionnée et l'autre une constante) alors la relation $\text{\sc id}_{ref,\pi_2}$ n'est pas vérifiable (fausse).

Par conséquent, si x₁ est 'couteau' dans t₁ et y₁ est 'couteau' dans t₂, alors les deux relations r_x=(x₁, x₂, x₃) et r_y=(y₁, y₂, y₃) sont comparables par rapport à leur première projection : $\text{\sc id}_{ref,\pi_1}(r_x, r_y)$ est vraie, même si $r_x\not=r_y$