Remarques sur l'écriture des formules

 

Dans la suite nous allons utiliser une notation générique (e) pour toute entité positionnée appartenant à l'ensemble $\mathit{Lp}\cup \mathit{Tp}\cup \mathit{Ap}$des entités positionnées. C'est pourquoi nous avons besoin de deux opérateurs qui nous donnent :

• le type formel de l'entité, c.-à-d. si l'entité est une lexie, un texte ou une anagnose :

  
  

  $$\mathit{tf}(e)=\left\{ \begin{array}{ll} L,& \text{si } e\i... ...t{Ap}\\ \textit{indéfini},& \text{sinon} \end{array}\right.$$
  
  
  avec L,T,A des constantes, comme pour le cas de l'indice L dans $\text{\sc ref}_L(l)$. De cette façon nous pouvons écrire $ec=\text{\sc ref}_{\mathit{tf}(e)}(e)$ et récupérer, dans ec, l'entité du corpus correspondant à e, c.-à-d. si $e=l\equiv(lc, p, t)$ alors $ec=\text{\sc ref}_{\mathit{tf}(e)}(e)=lc$

• le type formel de l'entité directement englobante, ou type parent : p(e), i.e.
  
  $$p(e)=\left\{ \begin{array}{ll} T,& \text{si } e\in \mathit{... ...t{Tp}\\ \textit{indéfini},& \text{sinon} \end{array}\right.$$
  
  
  de manière à pouvoir écrire $ep=\text{\sc ref}_{p(l)}(l)$ pour avoir ep=t au cas où $l\equiv(lc, p, t)$.

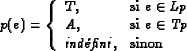
Pour alléger l'écriture, si $l\equiv(lc, p_l, t)$, $t\equiv(tc, p_t, a)$ sont deux entités appartenant à $\mathit{Lc}$ et $\mathit{Tc}$ respectivement, et si les fonctions suivantes ont un sens (c.-à-d. s'il n'existe pas de parties indéfinies), alors nous noterons :

$\text{\sc ref}(e)$	au lieu de	$\text{\sc ref}_{\mathit{tf}(e)}(e)$	e.g. $\text{\sc ref}(l)=lc$
$\text{\sc ref}_p(e)$	au lieu de	$\text{\sc ref}_{p(e)}(e)$	e.g. $\text{\sc ref}_p(l)=t$
$\text{\sc ref}_{pp}(e)$	au lieu de	$\text{\sc ref}_p(\text{\sc ref}_p(e))$	e.g. $\text{\sc ref}_{pp}(l)=a$
$\text{\sc ref}_{ppp}(e)$	au lieu de	$\text{\sc ref}_p(\text{\sc ref}_p(\text{\sc ref}_p(e)))$	e.g. $\text{\sc ref}_{ppp}(l)={\cal A}$

De même pour les identités :

$${\text{\sc id}_{ref}}(e_1, e_2) \Longleftrightarrow \text{\sc ref}(e_1)=\text{\sc ref}(e_2)$$

et

$${\text{\sc id}_{ref}}_p(e_1, e_2)\Longleftrightarrow\text{\sc ref}_p(e_1)=\text{\sc ref}_p(e_2)$$