



Rappelons que l'opérateur de construction  de SST est défini
pour un type
de SST est défini
pour un type
 et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.
et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.![[*]](images/cross_ref_motif.gif) ) :
) :
avec les contraintes mentionnées en
p.![[*]](images/cross_ref_motif.gif) .
.
Pour définir l'opérateur  ,
il suffit de préciser, pour un
type c et un ensemble P, un ensemble de SST qui respectent les
contraintes imposées à la p.
,
il suffit de préciser, pour un
type c et un ensemble P, un ensemble de SST qui respectent les
contraintes imposées à la p.![[*]](images/cross_ref_motif.gif) .
.
En fait, pour définir une SST qui appartient au résultat de
l'opérateur
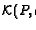 nous allons utiliser un sous ensemble de
l'information présente dans l'ensemble P. Au lieu d'utiliser la CS
nous allons utiliser un sous ensemble de
l'information présente dans l'ensemble P. Au lieu d'utiliser la CS
 entière, nous prenons en compte
seulement la SST
entière, nous prenons en compte
seulement la SST
 de la CS, telle que
de la CS, telle que
De cette façon la construction dépend seulement de la SST effective
de chacune des CS de P et non pas des CS-interprétants qui ont
permis la construction de cette CS. La définition est donc
non-récursive : elle manipule des SST et génère des SST.
D'autre part, les éléments << catalyseurs >>
 servent
à effectuer la << connexion >> ou << liaison >> entre l'information
sémique de
servent
à effectuer la << connexion >> ou << liaison >> entre l'information
sémique de
 et l'entité positionnée ej où cette
information sera attribuée. Nous rappelons que
e1, ..., em seront
les éléments effectifs de la CS résultat. Chaque e'j doit
donc être remplacée par l'entité ej correspondante dans les
SST-sources, afin que la SST-résultat concerne effectivement les
entités
e1, ..., ej.
et l'entité positionnée ej où cette
information sera attribuée. Nous rappelons que
e1, ..., em seront
les éléments effectifs de la CS résultat. Chaque e'j doit
donc être remplacée par l'entité ej correspondante dans les
SST-sources, afin que la SST-résultat concerne effectivement les
entités
e1, ..., ej.
Pour ce remplacement nous utilisons l'opérateur de substitution
symbolique sur toutes les SST en substituant chaque apparition d'une
entité << catalyseur >>
 par l'entité positionnée
correspondante :
par l'entité positionnée
correspondante :
 .
Les SST sources
.
Les SST sources
 sont transformées par conséquent en un nouvel ensemble de
SST effectives,
sont transformées par conséquent en un nouvel ensemble de
SST effectives,
 ,
définies comme suit :
,
définies comme suit :
pour

Nous sommes à présent prêts pour définir le fonctionnement de l'opérateur
 :
:
 l'une des conditions suivantes est vraie :
l'une des conditions suivantes est vraie :
- *
- construction d' attribution sémique triviale, c.-à-d. une construction qui produit une
SST avec une seule RE. Construction simpliste mais nécessaire,
surtout lors des essais interprétatifs rapides et pour une
interprétation directe ( CS de niveau k=0) d'un présupposé dans le
dictionnaire personnel (cf. 5).
Formellement,
 et :
et :
- 1.
- il y a une seule source sémique :
m=1
- 2.
- il y a une seule RE dans la SST finale :
- 3.
- l'élément effectif de la SST source (
 )
est présent
dans cette RE:
)
est présent
dans cette RE:
- 4.
- la SST finale a un seul élément effectif, compatible avec la
contrainte imposée à la p.
![[*]](images/cross_ref_motif.gif) :
:
- 5.
- les éléments de la SST sont tous les éléments de la RE
:
- *
- construction isotopique. La première d'un ensemble de
constructions similaires, concernant des SST avec un trait commun
entre toutes les RE. Une construction isotopique peut être :
- faible ou forte, selon la ressemblance entre les
RE de la SST et
- partielle ou complète, selon l'utilisation des
sources sémiques effectives :
ce qui fait quatre constructions isotopiques possibles.
Dans un premier temps nous examinons une construction isotopique
faible et partielle, cf. la fig. 4.9
Formellement,
 et
et
- 1.
- (contr. de ``déjà vu'' )
r1, ..., rk sont directement issues
des SST sources, après les opérations de substitution donnant
les
 :
:
et
Ceci garantit la contrainte suivante :
Bien sûr,  car sinon la construction est une attribution
triviale (cf.
car sinon la construction est une attribution
triviale (cf.
 ).
).
- 2.
- (contr. de ``participation'' ) au moins une RE de chaque SST
participe à la construction de la SST finale et l'élément
effectif de chacune des SST sources effectives est inclus dans au moins une
RE de la SST finale :
Cette contrainte permet d'établir l'ensemble des éléments
effectifs de la SST finale à la manière de la
contr. de ``constitution des éléments effectifs'', p.![[*]](images/cross_ref_motif.gif) .
.
- 3.
- (contr. de ``partialité'' ) au moins une RE d'au moins une SST ne
participe pas à la construction de la SST finale (c'est le sens
d'une construction << partielle >>) :
- 4.
- (contr. de ``comparaison de la proj. 3'' ) les troisièmes projections
des RE ont la même référence au corpus :
C'est la
propriété principale correspondant aux types
et
(<< faible >> et << isotopique >>, car nous
ne comparons que les troisièmes projections, et que les troisièmes
projections font toutes référence à une seule entité du corpus)
- 5.
- (contr. de ``faiblesse'' ) au moins une RE de la SST finale a une
deuxième projection différente de celle d'au moins une autre RE
de la SST (sinon la construction devient forte, cf. la contr. de ``comparaison des proj. 2 et 3'', p.
![[*]](images/cross_ref_motif.gif) ) :
) :
( étant le symbole de la négation logique)
étant le symbole de la négation logique)
- 6.
- la SST résultat est maximale par rapport à cette
propriété, c.-à-d. toutes les RE qui ont cette propriété sont
incluses dans la SST finale (
 )
:
)
:
- (a)
-

- (b)
-

- (c)
-

- (d)
-

- 7.
- (contr. de ``constitution des éléments effectifs'' ) les éléments
effectifs de la SST sont déterminés par la contrainte
p.
![[*]](images/cross_ref_motif.gif) :
:
- 8.
- (contr. de ``constitution des éléments'' ) les éléments de la SST
résultat sont déterminés par les éléments des RE qui sont déjà
définis :
Figure:
Présentation schématique d'une SST de
lexies, (mono)isotopique et faible. Ses éléments effectifs sont les
lexies
l1, l2, l3, positionnées toutes dans le même texte t1 de l'anagnose a1. Par contre, les informations sémiques peuvent
provenir d'autres contextes (une fois que l'opérateur de liaison
intertextuelle (
 )
a autorisé les passages intertextuels
concernant chacun des éléments effectifs)
)
a autorisé les passages intertextuels
concernant chacun des éléments effectifs)
 |
La structure se présente schématiquement comme sur la
fig.4.9
- *
-
 (construction isotopique, forte et
partielle) et :
(construction isotopique, forte et
partielle) et :
- 1.
- les RE de
 sont issues des SST sources (après
substitution), cf. la contr. de ``déjà vu'', p.
sont issues des SST sources (après
substitution), cf. la contr. de ``déjà vu'', p.![[*]](images/cross_ref_motif.gif)
- 2.
- au moins une RE de chaque SST participe à la construction,
cf. la contr. de ``participation'', p.
![[*]](images/cross_ref_motif.gif)
- 3.
- il s'agit d'une construction << partielle >>, donc la
contr. de ``partialité'', p.
![[*]](images/cross_ref_motif.gif) est ici aussi applicable
est ici aussi applicable
- 4.
- (contr. de ``comparaison des proj. 2 et 3'' ) les deuxièmes et
troisièmes projections des RE sont comparées par rapport à leur
référence au corpus :
- 5.
- la SST finale est maximale par rapport à la
propriété contr. de ``comparaison des proj. 2 et 3'', p.
![[*]](images/cross_ref_motif.gif) :
:
- (a)
-

- (b)
-

- (c)
-

- (d)
-

Figure 4.10:
Présentation schématique d'une SST de
lexies, (mono)isotopique et forte. Les éléments effectifs (
l1,
l2, l3) sont reliés par le même type de RE à la même entité
non positionnée lc. Ces relations sont issues de RE de
différents contextes.
 |
Pour un exemple de schématisation d'une SST isotopique forte
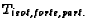 voir la fig. 4.10
voir la fig. 4.10
- 6.
- les éléments effectifs de la SST finale sont calculés de la
même manière que dans la contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif)
- 7.
- les éléments de la SST finale sont déterminés comme dans
la contr. de ``constitution des éléments'', p.
![[*]](images/cross_ref_motif.gif)
- *
-
 (construction isotopique, faible et
complète) et :
(construction isotopique, faible et
complète) et :
- 1.
- les RE sont issues des sources sémiques (
 )
par substitution, cf. la contr. de ``déjà vu'', p.
)
par substitution, cf. la contr. de ``déjà vu'', p.![[*]](images/cross_ref_motif.gif)
- 2.
- au moins une RE de chaque SST participe à la construction de
la SST résultat, cf. la contr. de ``participation'', p.
![[*]](images/cross_ref_motif.gif)
- 3.
- (contr. de ``complétude'' ) tous les éléments des SST
sources effectives (
 )
participent à la SST finale (
)
participent à la SST finale (
 )
(construction << complète >>) :
)
(construction << complète >>) :
- 4.
- seules les troisièmes projections sont comparées (construction
<< faible >>, cf. la contr. de ``comparaison de la proj. 3'', p.
![[*]](images/cross_ref_motif.gif) )
)
- 5.
- au moins une deuxième projection est différente des autres
(sinon la construction serait forte), cf. la
contr. de ``faiblesse'', p.
![[*]](images/cross_ref_motif.gif)
- 6.
- la maximalité est garantie par le fait que la construction est
<< complète >>
- 7.
- les éléments effectifs sont définis par la
contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif) et
et
- 8.
- les éléments en général sont définis par la
contr. de ``constitution des éléments'', p.
![[*]](images/cross_ref_motif.gif) .
.
- *
-
 (construction isotopique, forte et
complète) et :
(construction isotopique, forte et
complète) et :
- 1.
- les RE sont issues par substitution des sources sémiques
existantes, cf. la contr. de ``déjà vu'', p.
![[*]](images/cross_ref_motif.gif)
- 2.
- tous les éléments des SST sources effectives
(
 )
participent à la SST finale (
)
participent à la SST finale (
 )
(construction << complète >>, cf.. de ``complétude'', p.
)
(construction << complète >>, cf.. de ``complétude'', p.![[*]](images/cross_ref_motif.gif) )
)
- 3.
- les deuxièmes et troisièmes projections des RE sont
comparées par rapport à leur référence au corpus,
cf. la contr. de ``comparaison des proj. 2 et 3'', p.
![[*]](images/cross_ref_motif.gif)
- 4.
- la maximalité est garantie par le fait que la construction est
<< complète >>, cf. la contr. de ``complétude'', p.
![[*]](images/cross_ref_motif.gif)
- 5.
- les éléments effectifs sont définis par la
contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif) et
et
- 6.
- les éléments en général sont définis par la
contr. de ``constitution des éléments'', p.
![[*]](images/cross_ref_motif.gif)
- *
- construction transitive, c.-à-d. un ensemble
d'attributions sémiques indirectes d'un trait sémantique, par
l'intermédiaire d'autres attributions sémiques qui forment une chaîne liée, cf. la fig. 4.11.
Figure 4.11:
Un exemple de construction transitive,
où l'on peut voir la chaîne liée de RE et la création de nouvelles
RE
 |
Par rapport aux constructions
isotopiques, ce type de construction a la particularité de créer des RE qui n'appartenaient pas avant à l'ensemble des
sources sémiques.
Formellement, dans ce cas, il faut que
 et que
les conditions suivantes soient remplies :
et que
les conditions suivantes soient remplies :
- 1.
- les RE de
 sont divisées en deux ensembles R1 et
R2 qui correspondent, le premier à l'information sémique
existante en forme de chaîne liée et R2 aux nouvelles RE
créées par << transitivité >>. Donc :
sont divisées en deux ensembles R1 et
R2 qui correspondent, le premier à l'information sémique
existante en forme de chaîne liée et R2 aux nouvelles RE
créées par << transitivité >>. Donc :
avec R1, R2, conformes aux contraintes qui suivent :
- 2.
- les RE dans R1 sont toujours issues par substitution des
sources sémiques existantes, c.-à-d. elles obéissent à la
contr. de ``déjà vu'', p.
![[*]](images/cross_ref_motif.gif)
- 3.
- au moins une RE et l'élément effectif (
 )
de
chaque SST source participe à la construction, cf. la
contr. de ``participation'', p.
)
de
chaque SST source participe à la construction, cf. la
contr. de ``participation'', p.![[*]](images/cross_ref_motif.gif) . m doit être supérieur à 1, parce que
la chaîne comprend au moins 2 RE
. m doit être supérieur à 1, parce que
la chaîne comprend au moins 2 RE
- 4.
- les RE dans R1 sont liées, ce qui, plus concrètement,
veut dire que :
- (a)
- toutes ces RE ont une deuxième
projection (
 )
qui est une primitive appartenant à un
ensemble de primitives
)
qui est une primitive appartenant à un
ensemble de primitives
 permettant la
transitivité, c.-à-d. la génération de nouvelles RE comme nous
décrivons plus bas (cf. la définition de R2) :
permettant la
transitivité, c.-à-d. la génération de nouvelles RE comme nous
décrivons plus bas (cf. la définition de R2) :
avec
 configuré en général par
l'utilisateur qui a toujours la possibilité d'ajouter de nouvelles
primitives. Dans un premier temps :
configuré en général par
l'utilisateur qui a toujours la possibilité d'ajouter de nouvelles
primitives. Dans un premier temps :
- (b)
- ces RE sont liées, l'une après l'autre, comme le montre la
fig. 4.11. Le lien entre une RE et la RE
suivante dans la chaîne est, bien sûr, l'entité positionnée qui
se trouve en troisième projection de l'une et en première
projection de l'autre. Ces deux entités positionnées ne doivent
pas forcément être identiques (même entité type et même position
dans la même entité englobante). Comme pour l'attribution
sémique, nous appliquons l'opérateur de liaison
intertextuelle. Seulement, dans ce cas, nous exigeons une
liaison plus forte, exprimée, dans le cas général où les deux
entités sont de même niveau, par la contrainte que toutes deux
doivent être positionnées dans la même entité englobante (e.g. dans le même texte s'il s'agit de deux lexies, dans la même
anagnose s'il s'agit de deux textes). Dans le cas des
liaisons texte-lexie et anagnose-lexie, la contrainte est que la
lexie doit être positionnée dans la même anagnose et dans la
même racine
 ,
respectivement.
,
respectivement.
Ce qui est à noter dans les cas mixtes (texte-lexie,
anagnose-lexie) c'est que la liaison doit se faire dans la
direction texte vers lexie ou anagnose vers lexie et
non pas l'inverse. En d'autres termes, la transitivité opère en
une seule direction, elle peut seulement << passer >> la charge
sémique attribuée à la lexie (qui fait référence au texte ou à
l'anagnose) vers ce texte ou cette anagnose et non pas
l'inverse.
Par exemple, s'il est dit dans un commentaire que tel texte
constitue un pastiche et que dans le commentaire le pastiche est
un genre négativement caractérisé, cette négativité peut passer
au texte.
Ces RE doivent donc pouvoir être ordonnées de 1 jusqu'à la
taille de R1 (|R1| plus précisément) pour former une chaîne liée de la manière suivante :
avec, donc, la fonction de liaison forte entre deux
entités positionnées  et
et  ,
définie comme
suit :
,
définie comme
suit :
Nous remarquons que l'ordre de  et
et  est
important, car la liaison forte n'est pas symétrique dans
le cas d'un texte et d'une lexie, ou d'une anagnose et d'une
lexie
est
important, car la liaison forte n'est pas symétrique dans
le cas d'un texte et d'une lexie, ou d'une anagnose et d'une
lexie
- 5.
- Nous allons maintenant construire l'ensemble R2.
R2 est constitué de toutes les nouvelles RE issues des
opérations transitives entre les RE de R1, en commençant
toujours par la dernière sur la chaîne (i.e. la rn, si l'on
prend en compte la numérotation des RE dans R1). Donc, si nous
appelons z la deuxième projection de n'importe quelle RE dans
R1 (toutes les deuxièmes projections sont identiques, selon une
contrainte précédente) et y la troisième projection de la
dernière projection de la chaîne, celle qui va être transitivement
transférée à toutes les RE de R2, c.-à-d.
 et
et
 ,
alors R2 est défini comme suffit :
,
alors R2 est défini comme suffit :
avec
Il est évident que
|R2|=|R1|-1, donc avec une telle
construction le nombre des relations initiales est pratiquement
redoublé
- 6.
- la chaîne construite est maximale pour le trait choisi
(c.-à-d. l'entité
 ), au sens où elle ne peut pas être
étendue vers << la gauche >> à l'aide de relations se trouvant
parmi les sources sémiques effectives (
), au sens où elle ne peut pas être
étendue vers << la gauche >> à l'aide de relations se trouvant
parmi les sources sémiques effectives (
 )
:
)
:
avec r1 la première
relation de la chaîne

- 7.
- les éléments effectifs de la SST finale sont calculés de la
même manière que dans la contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif)
- 8.
- les éléments de la SST finale sont déterminés comme dans
la contr. de ``constitution des éléments'', p.
![[*]](images/cross_ref_motif.gif)
- *
- construction d'un graphe thématisé simple, c.-à-d. un
ensemble de RE liées entre elles à l'aide des éléments
effectifs communs, cf. fig. 4.12
Figure:
Un exemple de graphe thématisé
simple. Chaque RE possède au moins un élément effectif commun avec
au moins une autre RE. Par exemple, si l'on substitue à l1 'ta
beauté', à l2 'rend éprise, prise, au martyre étreinte', à l3 'ses rais, son ret, la crainte', à l4 'l'âme', alors on obtient
le graphe thématisé de la
fig.4.13
 |
Figure:
Graphe thématisé, issu de l'analyse de
Lune, Diane, Hécate, de Étienne Jodelle, présentée dans
[57, p.113]. a : `ta beauté' ; o : `rend éprise,
prise, au martyre étreinte' ; g : `l'âme' ; h : `ses rais, son
ret, la crainte'. Le graphe est retrouvé en p.127 de
[57]
 |
Formellement,
 et :
et :
- 1.
- les RE sont directement issues des sources sémiques par
substitution ; par conséquent la contr. de ``déjà vu'', p.
![[*]](images/cross_ref_motif.gif) , est appliquée
, est appliquée
- 2.
- tous les éléments effectifs et les SST sources y participent
; ainsi la construction doit respecter la contr. de ``participation'', p.
![[*]](images/cross_ref_motif.gif)
- 3.
- la SST résultat doit avoir une forme de graphe dont le type
est généralement paramétré, par rapport aux deuxièmes projections
(
 )
des RE et à leur organisation. Ici nous
montrons la définition de la construction pour le graphe de la
fig. 4.12 :
)
des RE et à leur organisation. Ici nous
montrons la définition de la construction pour le graphe de la
fig. 4.12 :
avec les << types >> suivants de RE 4.17 :
et avec les liaisons suivantes entre RE:
- 4.
- les éléments effectifs sont déterminées de la manière
habituelle, par contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif)
- 5.
- de même, les éléments de la SST finale, par la
contr. de ``constitution des éléments'', p.
![[*]](images/cross_ref_motif.gif)
- *
- construction d'actant, c.-à-d. ensemble des traits caractérisant un même élément effectif, cf. fig. 4.14
Figure:
Un exemple de SST de type
 .
Tous les traits sémantiques concernent
un élément effectif central. Ils peuvent être considérés comme de
rôles différents d'un même actant.
.
Tous les traits sémantiques concernent
un élément effectif central. Ils peuvent être considérés comme de
rôles différents d'un même actant.
 |
Formellement,
 et :
et :
- 1.
- les RE sont directement issues des sources sémiques par
substitutions donnant
 ,
donc il faut
appliquer la contr. de ``déjà vu'', p.
,
donc il faut
appliquer la contr. de ``déjà vu'', p.![[*]](images/cross_ref_motif.gif)
- 2.
- les éléments effectifs dans P ainsi qu'au moins une RE de
chacune des SST sources effectives participent à la SST finale, cf. contr. de ``participation'', p.
![[*]](images/cross_ref_motif.gif)
- 3.
- les RE concernent des rôles standards de l' actant, i.e. des rôles issus des relations primitives de
l'ensemble
 :
:
- 4.
- il s'agit bien sûr du même << actant >> :
Nous faisons ici
référence aux relations présentées dans la
fig.4.12. Une autre convention concernant
l'orientation des flèches, conduirait au remplacement de la
troisième projection, dans ce cas précis, par la première
projection
 .
.
- 5.
- les RE sont situées dans le texte même, autrement dit, le
contexte de cette construction ne dépasse pas le texte :
- 6.
- les éléments effectifs sont calculés de la manière standard,
cf. la contr. de ``constitution des éléments effectifs'', p.
![[*]](images/cross_ref_motif.gif)
- 7.
- de même pour les éléments, cf. la contr. de ``constitution des
éléments'', p.
![[*]](images/cross_ref_motif.gif)
Nous devons remarquer que toutes ces constructions génèrent des SST
correspondant à des CS de niveau k>0. Nous rappelons que les CS de
niveau k=0 sont toutes définies par l'utilisateur. Dans ce cas, le
système doit juste vérifier si les contraintes que le type c pose à
la SST sont respectées. En effet, pour une CS de niveau k=0, il
est simplement vérifié que :
avec
 la SST finale et c son
type, donnés au système (e.g. déterminés par l'utilisateur), et
la SST finale et c son
type, donnés au système (e.g. déterminés par l'utilisateur), et
où
 sont les
éléments effectifs de la SST, également considérés comme donnés au
système. La vérification prend en compte toutes les contraintes
présentées plus haut sauf, bien sûr, celles qui utilisent les SST
sources effectives (
sont les
éléments effectifs de la SST, également considérés comme donnés au
système. La vérification prend en compte toutes les contraintes
présentées plus haut sauf, bien sûr, celles qui utilisent les SST
sources effectives (
 ), qui, dans le cas d'une
CS de niveau k=0, ne sont pas définies.
), qui, dans le cas d'une
CS de niveau k=0, ne sont pas définies.




Theodore Thlivitis, 1998
 de SST est défini
pour un type
de SST est défini
pour un type
 et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.
et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.![[*]](images/cross_ref_motif.gif) ) :
) :
 de SST est défini
pour un type
de SST est défini
pour un type
 et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.
et un ensemble P d'<< informations
sémiques >>, provenant de différentes CS (cf. p.![[*]](images/cross_ref_motif.gif) ) :
) :
![[*]](images/cross_ref_motif.gif) .
.
 ,
il suffit de préciser, pour un
type c et un ensemble P, un ensemble de SST qui respectent les
contraintes imposées à la p.
,
il suffit de préciser, pour un
type c et un ensemble P, un ensemble de SST qui respectent les
contraintes imposées à la p.![[*]](images/cross_ref_motif.gif) .
.
![]() nous allons utiliser un sous ensemble de
l'information présente dans l'ensemble P. Au lieu d'utiliser la CS
nous allons utiliser un sous ensemble de
l'information présente dans l'ensemble P. Au lieu d'utiliser la CS
![]() entière, nous prenons en compte
seulement la SST
entière, nous prenons en compte
seulement la SST
 de la CS, telle que
de la CS, telle que
![]() servent
à effectuer la << connexion >> ou << liaison >> entre l'information
sémique de
servent
à effectuer la << connexion >> ou << liaison >> entre l'information
sémique de
 et l'entité positionnée ej où cette
information sera attribuée. Nous rappelons que
e1, ..., em seront
les éléments effectifs de la CS résultat. Chaque e'j doit
donc être remplacée par l'entité ej correspondante dans les
SST-sources, afin que la SST-résultat concerne effectivement les
entités
e1, ..., ej.
et l'entité positionnée ej où cette
information sera attribuée. Nous rappelons que
e1, ..., em seront
les éléments effectifs de la CS résultat. Chaque e'j doit
donc être remplacée par l'entité ej correspondante dans les
SST-sources, afin que la SST-résultat concerne effectivement les
entités
e1, ..., ej.
![]() par l'entité positionnée
correspondante :
par l'entité positionnée
correspondante :
![]() .
Les SST sources
.
Les SST sources
![]() sont transformées par conséquent en un nouvel ensemble de
SST effectives,
sont transformées par conséquent en un nouvel ensemble de
SST effectives,
![]() ,
définies comme suit :
,
définies comme suit :

 :
:
![]() l'une des conditions suivantes est vraie :
l'une des conditions suivantes est vraie :
![]() et :
et :
 )
est présent
dans cette RE:
)
est présent
dans cette RE:
![[*]](images/cross_ref_motif.gif) :
:
![]() et
et
 car sinon la construction est une attribution
triviale (cf.
car sinon la construction est une attribution
triviale (cf.
![]() ).
).
![[*]](images/cross_ref_motif.gif) .
.
![[*]](images/cross_ref_motif.gif) ) :
) :
 étant le symbole de la négation logique)
étant le symbole de la négation logique)
 )
:
)
:


![[*]](images/cross_ref_motif.gif) :
:

 sont issues des SST sources (après
substitution), cf. la contr. de ``déjà vu'', p.
sont issues des SST sources (après
substitution), cf. la contr. de ``déjà vu'', p.![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif) est ici aussi applicable
est ici aussi applicable
![[*]](images/cross_ref_motif.gif) :
:



![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
 )
participent à la SST finale (
)
participent à la SST finale (
 )
(construction << complète >>) :
)
(construction << complète >>) :
![[*]](images/cross_ref_motif.gif) )
)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif) et
et
![[*]](images/cross_ref_motif.gif) .
.
![[*]](images/cross_ref_motif.gif)
 )
(construction << complète >>, cf.. de ``complétude'', p.
)
(construction << complète >>, cf.. de ``complétude'', p.![[*]](images/cross_ref_motif.gif) )
)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif) et
et
![[*]](images/cross_ref_motif.gif)

![]() et que
les conditions suivantes soient remplies :
et que
les conditions suivantes soient remplies :
 sont divisées en deux ensembles R1 et
R2 qui correspondent, le premier à l'information sémique
existante en forme de chaîne liée et R2 aux nouvelles RE
créées par << transitivité >>. Donc :
sont divisées en deux ensembles R1 et
R2 qui correspondent, le premier à l'information sémique
existante en forme de chaîne liée et R2 aux nouvelles RE
créées par << transitivité >>. Donc :
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif) . m doit être supérieur à 1, parce que
la chaîne comprend au moins 2 RE
. m doit être supérieur à 1, parce que
la chaîne comprend au moins 2 RE
 )
qui est une primitive appartenant à un
ensemble de primitives
)
qui est une primitive appartenant à un
ensemble de primitives
 ,
respectivement.
,
respectivement.
 et
et  ,
définie comme
suit :
,
définie comme
suit :

 et
et  est
important, car la liaison forte n'est pas symétrique dans
le cas d'un texte et d'une lexie, ou d'une anagnose et d'une
lexie
est
important, car la liaison forte n'est pas symétrique dans
le cas d'un texte et d'une lexie, ou d'une anagnose et d'une
lexie
![]() et
et
![]() ,
alors R2 est défini comme suffit :
,
alors R2 est défini comme suffit :
 ), au sens où elle ne peut pas être
étendue vers << la gauche >> à l'aide de relations se trouvant
parmi les sources sémiques effectives (
), au sens où elle ne peut pas être
étendue vers << la gauche >> à l'aide de relations se trouvant
parmi les sources sémiques effectives (

![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)


![]() et :
et :
![[*]](images/cross_ref_motif.gif) , est appliquée
, est appliquée
![[*]](images/cross_ref_motif.gif)
 )
des RE et à leur organisation. Ici nous
montrons la définition de la construction pour le graphe de la
fig. 4.12 :
)
des RE et à leur organisation. Ici nous
montrons la définition de la construction pour le graphe de la
fig. 4.12 :
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)

![]() et :
et :
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
 :
:
 .
.
![[*]](images/cross_ref_motif.gif)
![[*]](images/cross_ref_motif.gif)
 la SST finale et c son
type, donnés au système (e.g. déterminés par l'utilisateur), et
la SST finale et c son
type, donnés au système (e.g. déterminés par l'utilisateur), et