Liaison intertextuelle

 

L'opérateur de liaison intertextuelle ( ${\mathcal L}$) est défini relativement à une entité positionnée, e, et une classe attribuante $\mathit{T}_a(e', \mathit{int}^{(k')})$.

Le rôle d'un tel opérateur est fondamental pour une interprétation intertextuellement fondée. Sa mise en uvre est plutôt une heuristique algorithmique qu'une définition formelle. Ici nous allons justifier les principaux points d'une première mise en place sans exclure un possible affinement dans le cas précis d'une utilisation particulière.

Dans le cadre de la constitution d'une nouvelle CS (et, par extension, dans toute interprétation), les entités textuelles (e.g. les lexies d'un texte) reçoivent des attributions sémiques. Cette phase du travail interprétatif est très importante mais impossible à prévoir informatiquement, car typiquement dépendant de la compétence interprétative d'un agent humain. Ce que nous proposons, au contraire, en incluant les interprétants (sous la forme de classes attribuantes) dans la description sémantique, c'est tout simplement d'inscrire cette phase importante au sein d'une description plus large, intertextuelle, et forcer l'utilisateur et lecteur d'expliciter les éléments de cette description, qui sont implicitement mis en uvre pas sa compétence interprétative. Cette explicitation doit être intrinsèque, i.e. doit utiliser des ressources sémantiques glanées à l'intérieur d'une anagnose définie.

Dans le processus de l'attribution sémique, une étape généralement implicite, mais informatiquement fondamentale, concerne le rapport entre la source d'information sémique utilisée lors d'une construction d'une CS et sa cible, l'entité textuelle, constituant un élément de la future CS. C'est dans l'objectif de pouvoir décrire cette relation, en principe intertextuelle comme on le verra, que nous avons besoin de l'opérateur de liaison intertextuelle.

Pour prendre un exemple, dans l'analyse du Salut de Mallarmé, dans [57], le trait sémantique /navigation/ est attribué à 'poupe' en raison de la mention maritime dans un dictionnaire. Accepté sans aucune difficulté par l'homme, le passage de /maritime/ à /navigation/ pour 'poupe' n'est pas direct pour le système informatique. Si l'on veut attribuer /navigation/ à 'poupe' il faut utiliser une source sémique où 'poupe' est directement liée à /navigation/ ; par exemple, en construisant une nouvelle classe qui prend en compte la relation entre 'maritime' et 'navigation' et entre 'poupe' et 'maritime', ou d'une autre manière, peu importe. Ce qui importe, c'est qu'à la fin de ce pré-travail, dans le dictionnaire, soit retrouvée ou constituée^4.11 une classe selon laquelle le trait /navigation/ est affecté à 'poupe'.

Pour pouvoir effectuer une attribution sémique, il faut donc, dans un premier temps, << normaliser >> la source par rapport à la cible. Ceci est généralement possible en utilisant une source sémique (i.e. une classe attribuante) avec une entité textuelle identique à l'entité textuelle cible, au sens où l'entité textuelle type est la même mais l'entité occurrence peut-être différente. Un premier indice de << liaison >> entre une source sémique ( $\mathit{T}_a(e', \mathit{int}^{(k')}$) et sa cible (e) est donc la relation ${\text{\sc id}_{ref}}$ entre les entités textuelles concernées, c.-à-d.

$${\text{\sc id}_{ref}}(e, e')$$

Dans un deuxième temps, en vertu d'un postulat de localité contextuelle, nous exigeons que les sources sémiques d'une attribution sémique et leurs cibles soient << textuellement >> proches : si le lecteur utilise une information sémique tirée de la note biographique sur l'auteur, alors il faudra qu'il incorpore cette note dans l'espace textuel de son analyse (son anagnose).

Ceci a un double avantage pour l'assistance :

• Le système informatique connaît que cette note est prise en compte et, donc, il pourra utiliser les classes sémantiques qui y sont éventuellement définies comme suggestions sémiques pour la constitution de nouvelles classes, ultérieurement. Il les considérera en priorité par rapport à d'autres possibles sources sémiques, venant de l'extérieur, en constituant de cette façon au soutien de la densité des relations au sein de l'espace textuel de l'analyse.
• Et d'autre part, précisément, en connaissant le cadre textuel des attributions sémiques, le système peut tenter une quantification de la cohérence de l'analyse en examinant la distribution des relations sémiques établies dans l'espace textuel de l'analyse (l'anagnose). Et ainsi, offrir un premier indice -- certes non définitif ni concluant -- du caractère productif ou descriptif de l'analyse.

Une telle localité contextuelle est établie dans le cas, par exemple, d'une attribution sémique où l'entité-cible (e) est une lexie $l=\left(lc, p_l, \left(tc, p_t, a\right)\right)$ et l'entité-source (e') est une autre lexie $l'=\left({lc}', p'_l, \left({tc}', p'_t, a'\right)\right)$, si les lexies sont situées dans des textes qui appartiennent au même espace textuel (c.-à-d. de textes situés dans la même anagnose).

Ce dernier, si on ne considère pas les positions des anagnoses, est noté ${\text{\sc id}_{ref}}(a,a')$.

Pour résumer, nous explicitons ici de façon formelle le postulat de localité textuelle pour deux entités positionnées e et e', faisant partie d'une attribution sémique représentée par le couple $(e, \mathit{T}_a(e', \mathit{int}^{(k')}))$. L'opérateur de liaison intertextuelle ( ${\mathcal L}$) sert précisément d'indice de cette localité textuelle. Comme nous l'avons déjà vu, la contrainte ${\mathcal L}>0$ est posée avant qu'une nouvelle attribution sémique soit effectuée dans le cadre de la construction d'une nouvelle CS.

La définition générale de l'opérateur ${\mathcal L}$ est la suivante :

$${\mathcal L}=c_0\cdot\Pi\cdot(1+\Sigma)$$

où

• c₀ est une constante qui sert à garder la valeur de ${\mathcal L}$ dans les limites [0,1] souhaitées ;
• $\Pi$ correspond à la partie << obligatoire >>, c.-à-d. la partie dont la valeur doit être supérieure à zéro pour que la liaison soit possible ;
• $\Sigma$ correspond à la partie << facultative >>, au sens où elle peut seulement améliorer une valeur de liaison qui est déjà supérieure à zéro. Les valeurs apportées par $\Sigma$ vont servir comme critères de classification de différentes attributions sémiques possibles.

La définition de $\Pi$ et $\Sigma$ dépend des types des entités e et e'. Nous distinguons cinq cas :

1.

$e,e'\in \mathit{Lp}$, donc

e=l=(lc,p_l,t)=(lc,p_l,(tc,p_t,a)) et

e'=l'=(lc',p'_l,t')=(lc',p'_l,(tc',p'_t,a'))

Dans ce cas :

$$\begin{array}{l} \Pi=\text{\sc Ref}_{\text{A}}(a,a')\cdot\te... ... Ref}_{\text{L}}(l,l')={\text{\sc id}_{ref}}(l,l') \end{array}$$

et

$$\begin{array}{l} \Sigma=c_1\cdot\text{\sc Ref}_{\text{T}}(t,... ...c id}_{ref}}(t,t')\cdot{\text{\sc id}_{pos}}(l,l') \end{array}$$

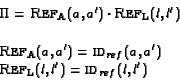
Nous rappelons que ${\text{\sc id}_{ref}}$ est définie comme une relation, donnant des valeurs vraies ou fausses. Pour simplifier l'expression des formules, nous utilisons la transformation, habituelle en informatique :

$$\begin{array}{lll} \text{Vrai} & \rightarrow & 1\\ \text{Faux} & \rightarrow & 0 \end{array}$$

${\text{\sc id}_{pos}}(e,e')$ est juste une relation d'identité entre les positions des entités positionnées e et e' relativement à l'entité englobante. Par exemple :

$${\text{\sc id}_{pos}}(l,l')=\left\{ \begin{array}{ll} 0 & \... ...} p_l=p'_l\\ 1 & \text{ si } p_l\not=p'_l \end{array}\right.$$

Les constantes c₁,...,c₇ sont définies selon l'importance relative que l'on veut donner aux différentes parties qui constituent la valeur finale de la liaison intertextuelle. Les valeurs dépendent de l'heuristique mise en uvre dans une application précise. Certes, si l'on veut que ${\mathcal L}$ prenne des valeurs dans l'intervalle [0,1] il faut postuler que :

$$c_0\cdot(1+c_1+c_2+c_3+c_4)\leq 1$$

Pour établir les parties concernant la position des lexies, des textes et des anagnoses, nous nous sommes appuyé sur un constat évident, exprimé déjà auparavant (cf. p.) et selon lequel on ne peut pas comparer les positions de deux entités si les entités ne sont pas positionnées dans la même entité englobante. Cette contrainte est appliquée à la définition de :

• $\text{\sc Pos}_{\text{T}}={\text{\sc id}_{ref}}(a,a')\cdot{\text{\sc id}_{pos}}(t,t')$ et
• $\text{\sc Pos}_{\text{L}}={\text{\sc id}_{ref}}(t,t')\cdot{\text{\sc id}_{pos}}(l,l')$

une position identique entre, par exemple, l et l', est prise en compte dans la valeur finale de la liaison intertextuelle seulement si les deux lexies sont positionnées dans un même texte ( ${\text{\sc id}_{ref}}(t,t')$). Pour deux anagnoses a et a' l'entité englobante est toujours la même (${\cal A}$), donc il suffit de comparer directement les positions $\text{\sc Pos}_{\text{A}}={\text{\sc id}_{pos}}(a,a')$

2.

$e,e'\in\mathit{Tp}$, donc

e=t=(tc, p_t, a) et

e'=t'=(tc', p'_t, a')

Le besoin d'une liaison intertextuelle est issu cette fois d'une attribution sémique dont les extrémités sont deux textes (le texte source et le texte cible) considérés en tant qu'unités ^4.12 : nous voulons << passer >> quelques traits sémantiques caractérisant un texte occurrence vers une autre occurrence du même texte type. Pour que ce passage ait un sens, nous exigeons la proximité des deux occurrences au sein de l'espace textuel de l'analyse. Puisque cet espace est l'anagnose, les deux textes doivent être placés dans la même anagnose. Nous avons alors :

$$\begin{array}{l} \Pi=\text{\sc Ref}_{\text{A}}(a,a')\cdot\text{\sc Ref}_{\text{T}}(t,t')\\ [5mm] \end{array}$$

et

$$\begin{array}{l} \Sigma=c_5\cdot\text{\sc Pos}_{\text{A}}(a,a')+c_6\cdot\text{\sc Pos}_{\text{T}}(t,t') \end{array}$$

Les définitions de $\text{\sc Ref}_{\text{A}}$, $\text{\sc Ref}_{\text{T}}$, $\text{\sc Pos}_{\text{A}}$ et $\text{\sc Pos}_{\text{T}}$ sont comme avant. De même les constantes c₅ et c₆ doivent remplir la contrainte :

$$c_0\cdot(1+c_5+c_6)\leq 1$$

Par exemple, si l'on considère que la proximité entre deux textes qui sont égaux est moins grande que la proximité entre deux lexies égales^4.13, on peut avoir c₅=c₂ et c₆=c₃. Mais la définition exacte est une question de l'application et des heuristiques mises en uvre.

3.

$e,e'\in\mathit{Ap}$, donc e=a et e'=a'. Dans ce cas, sans doute quelque peu trivial, car les anagnoses sont toujours positionnées dans la même entité englobante, nous ne devons contrôler que l'identité (par rapport au type) des deux anagnoses a et a' :

$$\begin{array}{l} \Pi=\text{\sc Ref}_{\text{A}}(a,a') \end{array}$$

et

$$\begin{array}{l} \Sigma=c_7\cdot\text{\sc Pos}_{\text{A}}(a,a') \end{array}$$

avec

$$c_0\cdot(1+c_7)\leq 1$$

Dans ce cas aussi, et selon toujours le même raisonnement, on pourrait poser c₇=c₂.

4.

$e\in\mathit{Tp}$ et $e'\in\mathit{Lp}$. Donc,

e=t=(tc, p_t, a) et

e'=l'=(lc',p'_l,t')=(lc',p'_l,(tc',p'_t,a'))

Il s'agit d'un cas mixte et assez spécial, puisque il est issu du besoin de surpasser les difficultés de l'utilisation d'un métalangage.

Le problème est le suivant : nous voulons pouvoir faire une attribution sémique sur un texte entier à partir d'une attribution sémique sur une lexie qui se réfère à ce texte.

Par exemple, supposons que dans une note écrite par l'auteur d'un texte, il est dit que le texte en question est un hommage à un tel autre auteur. Cette information, intéressante pour l'institution d'un certain nombre de relations intertextuelles, est attribuée sur une lexie de la note, mais concerne en effet le texte entier et devrait pouvoir y être attribuée.

L'importance de ce cas mixte de liaison intertextuelle, réside sur le fait qu'il donne la possibilité d'intégrer de tels traits sémantiques (issus d'attributions sémiques sur de lexies et concernant un texte entier) de façon naturelle parmi le reste des attributions sémiques.

Dans ce cas :

$$\begin{array}{l} \Pi=\text{\sc Ref}_{\text{A}}(a,a')\cdot\text{\sc Ref}_{\text{TL}}(t,l') \end{array}$$

et

$$\begin{array}{l} \Sigma=c_8\cdot\text{\sc Ref}_{\text{T}}(t,... ...}(a,a')+c_{10}\cdot\text{\sc Pos}_{\text{T}}(t,t') \end{array}$$

La proximité textuelle est calculée d'une façon pareille que pour les cas précédents, puisque le texte t et la lexie l sont des entités toujours positionnées. La nouveauté c'est $\text{\sc Ref}_{\text{TL}}(t, l')$, le facteur principal de la référence entre une lexie et un texte :

$$\text{\sc Ref}_{\text{TL}}(t, l')=\left\{ \begin{array}{ll} ... ... fait référence à $t$}\\ 0 & \text{sinon} \end{array}\right.$$

Les possibilités de référence étant infinies et informatiquement non identifiables (allant de la référence pronominale, jusqu'à la référence implicite), nous laissons à l'utilisateur le soin d'expliciter de tels rapprochements entre lexies et textes.

Une remarque importante ici concerne le fait qu'un tel rapprochement, même s'il n'est pas identique à la correspondance établie entre une lexie source et une lexie cible dans le cadre d'une attribution sémique, reste quand-même très proche, car il concerne une attribution sémique dont la source et la cible appartiennent au matériau textuel. Simplement, l'usage de la langue dans un texte permet les passages entre différents niveaux de textualité. Si on accepte que dans un espace textuel commun, une lexie peut apporter sa charge sémantique à une autre occurrence de la même lexie type, nous ne voyons pas pourquoi elle ne pourrait pas, de la même façon, apporter sa charge sémantique à un texte auquel elle se réfère. En ce qui concerne les constantes c₈, c₉, c₁₀ il faut, comme toujours, avoir

$$c_0\cdot(1+c_8+c_9+c_{10})\leq 1$$

Et pour garder l'uniformité avec le reste des mesures, on pourrait utiliser c₈=c₁, c₉=c₂ et c₁₀=c₃

5.

$e\in\mathit{Ap}$ et $e'\in\mathit{Lp}$, donc e=a et

e'=l'=(lc',p'_l,t')=(lc',p'_l,(tc',p'_t,a'))

Cette fois le passage se fait entre une lexie et une anagnose entière. Une telle attribution pourrait concerner le type d'analyse pratiqué dans une anagnose, ou décrire le fait qu'une analyse est fondé sur une telle autre analyse dont elle utilise les résultats.

Le point particulier par rapport au texte est que les lexies qui font référence à l'anagnose ne se trouvent pas normalement dans un texte analysé^4.14. Si c'est le lecteur (et utilisateur) qui crée l'anagnose, alors il est responsable des traits sémantiques par lesquels il la charge. Pour cette raison, il possède d'un texte spécial dans l'anagnose (une sorte de dictionnaire personnel ) qu'il peut enrichir d'informations qui lui semblent utiles. C'est principalement dans ce texte que vont se trouver des lexies qui font référence à l'anagnose et dont la charge sémantique peut passer à l'anagnose entière.

Les contraintes textuelles sont donc équivalentes à celles imposées dans le cas du texte, mais cette fois elles s'avèrent plus restreintes :

$$\begin{array}{l} \Pi=\text{\sc Ref}_{\text{A}}(a,a')\cdot\text{\sc Ref}_{\text{AL}}(a,l') \end{array}$$

et

$$\begin{array}{l} \Sigma=c_{11}\cdot\text{\sc Pos}_{\text{A}}(a,a') \end{array}$$

$\text{\sc Ref}_{\text{AL}}(a,l')$ est défini de la même manière que $\text{\sc Ref}_{\text{TL}}$ :

$$\text{\sc Ref}_{\text{AL}}(a, l')=\left\{ \begin{array}{ll} ... ...ait référence à $a$}\\ 0 & \text{sinon} \end{array}\right.$$

Et bien sûr, la constante c₁₁ peut être égale à c₉ et en général il faut que : $c_0\cdot(1+c_{11})\leq 1$